Метадинамика

Коллективные переменные

Полученное ФП сложно анализировать непосредственно, но из него можно выделить некоторое полезное подмножество координат, после чего сконструировать из них коллективные переменные \(\mathbf{S}=S_{1},\cdots,S_{d}\), позволяющие строить состоятельные утверждения о внутренних степенях свободы системы (например, белковой молекулы) и интерпретировать их.

Некоторые простые и их интерпретация1:

  • 1 для удобства нотации полезно ввести следующий формализм: совокупность КП \(\mathbf{S}=S_{1},\cdots,S_{d}\) будем называть пространством КП, конкретное значение \(S_{i}\) будем обозначать \(s_{i}\), вектор в пространстве \(\mathbf{S}\) запишем как \(\mathbf{s}=(s_{1},\cdots,s_{d})\), выражение \(\mathbf{S}(\mathbf{q})\) или \(\mathbf{S}(t)\equiv\mathbf{S}(\mathbf{q}(t))\) подчёркивает, что КП зависят от координат или времени соответственно

    1. расстояние между двумя атомами2 (или между центрами масс групп атомов) \(S=|\mathbf{r}_{i}-\mathbf{r}_{j}|\) — собственно расстояние или длина связи;

    2. угол между тремя атомами \(S=\widehat{{\bf r}_{i},{\bf r}_{j},{\bf r}_{k}}\) — валентный угол;

    3. двугранный угол, образованный четырьмя атомами, \(S=\widehat{{\bf r}_{i,j},{\bf r}_{k,l}}\) — торсионный угол;

    4. количество соседей внутри шара радиуса \(R\), описанного вокруг атома, \(S={\rm card}\left\{ \mathbf{r}_{i}\colon|\mathbf{r}_{i}-\mathbf{r}_{j}|\le R\right\} -1\) — координационное число, оператор «\(\text{{\rm card}}\)» обозначает размер множества.

  • 2 здесь и далее — не между произвольными атомами, а между наперёд заданными; \(\mathbf{r}_{i}\)— радиус-вектор \(i\)го атома, \({\bf r}_{i,j}\) — вектор c началом в \(i\)м и конце в \(j\)м атомах

    • Метадинамика [nwchemMeta?]

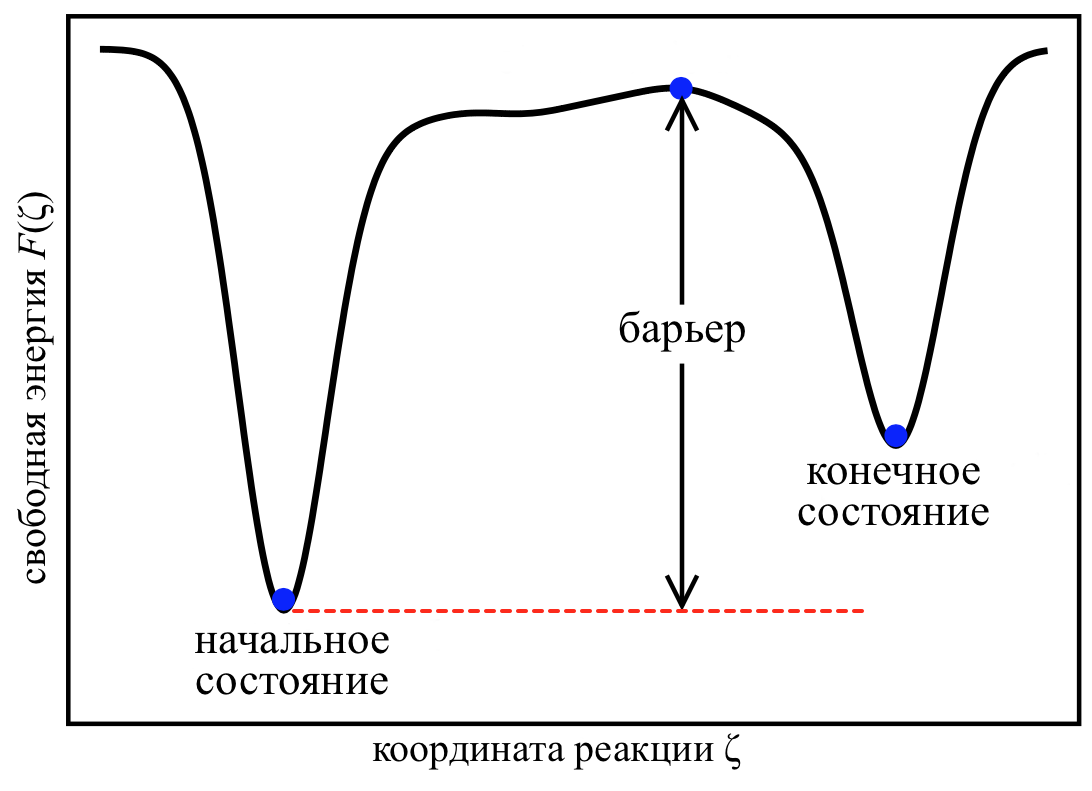
    Численный эксперимент МД ограничен доступным машинным временем, в нормальном случае его не хватит для исследования всего ФП, а если энергические барьеры между состояниями достаточно высоки, за время моделирования система может даже не покинуть начальную область ФП, пример системы, в которой может наблюдаться такая картина, приведён на Рис 6.1; подобный маловероятный «прыжок» молекулы из одного минимума в другой называют редким событием [1].

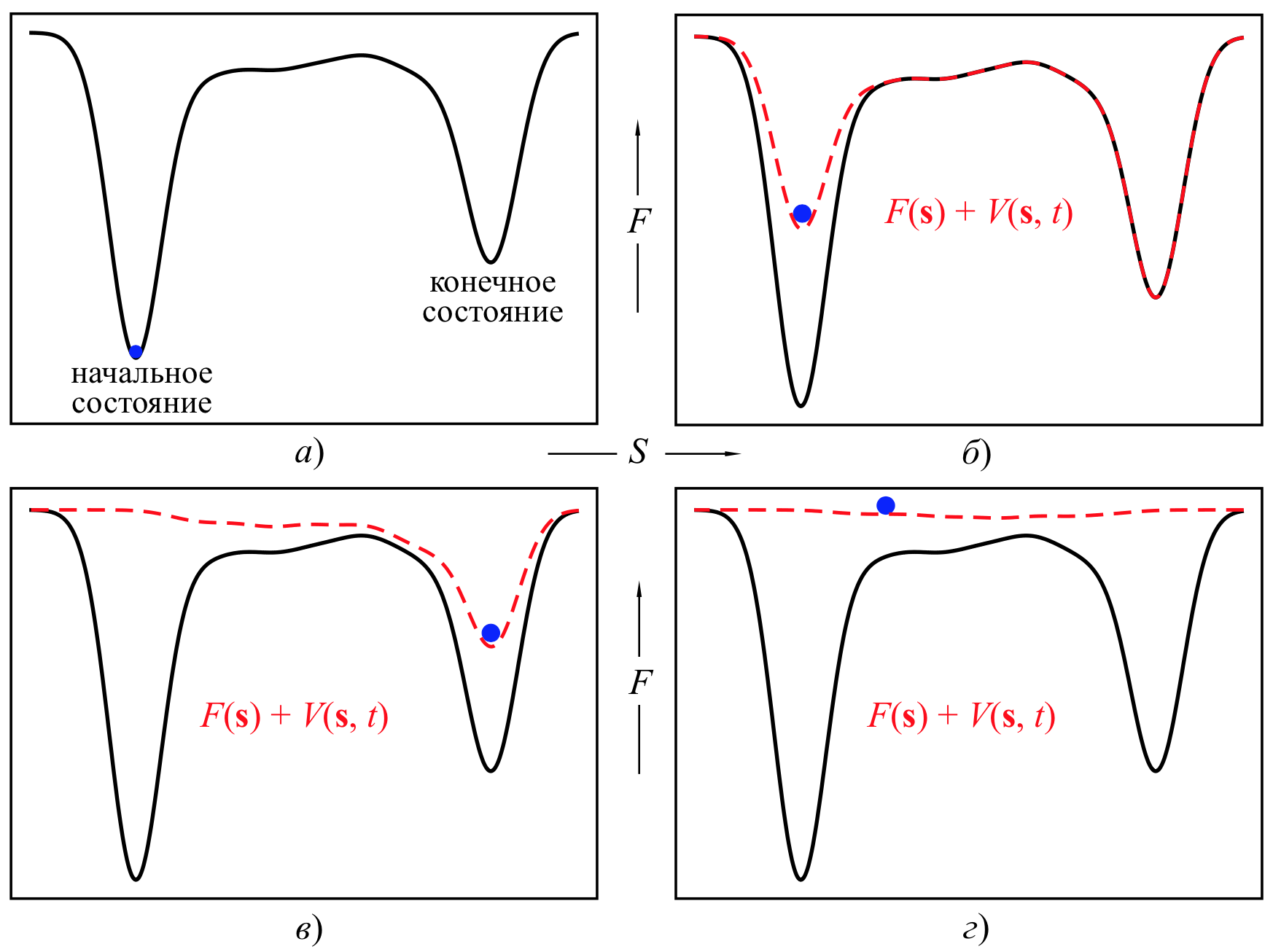
    Рисунок 6.1: Профиль свободной энергии

    Метадинамика — неравновесный метод молекулярного моделирования. Для эффективного получения выборки из ФП к потенциалам взаимодействия, описанным в [Описание метода], добавляют зависящий от КП3 \(\mathbf{S(q)}\) и времени \(t\) смещающий потенциал \(V(\mathbf{S(q)},t)\), который будет способствовать выходу системы из её энергетического минимума, что, в свою очередь, позволит исследовать новые области ФП.

  • 3 обозначения коллективных переменных были введены в Коллективные переменные

    • Для пространства \(\mathbf{S(q)}\) изменение потенциала \(V(\mathbf{S(q)},t)\) во времени происходит не непрерывно; в начале симуляции \(V(\mathbf{S(q)},t=0)=0\), однако через равные промежутки времени \(\tau\) к нему добавляются гауссовы функции так, чтобы положение их максимумов совпало с текущем значением коллективных переменных \(\mathbf{s}(t)\):

    \[V(t)=V(t-\tau)+h(t)\exp\left\{ -\dfrac{1}{2}\sum_{i=1}^{d}\left(\dfrac{s_{i}(t)-s_{i}(\lfloor t/\tau\rfloor\cdot\tau)}{\sigma_{i}}\right)^{2}\right\}\] или, если исключить предыдущее значение \(V(t-\tau)\) и суммировать по шагам \(k\) явно,

    \[V(\bf s,t)=\sum_{k=1}^{\lfloor t/\tau\rfloor}h(t)\exp\l\{ -\dfrac 1 2 \sum_{i=1}^d \l(\dfrac{s_i-s_i(k \tau)}{\sigma_i}\r)^2\r\} . \tag{6.1}\]

    Рисунок 6.2: Этапы наложения гауссиан в процессе метадинамики: а) начало симуляции; б) выход из области начального состояния; в) исследование области конечного состояния; г) свободное плавание

    Накачку системы энергией называют нагреванием, поскольку в процессе температура неизбежно возрастёт на фиктивную величину \(\Delta T\); если в начальный момент система условно находилась в нуле энергии, то в ходе нагрева ей становятся доступны состояния со свободной энергией \([0\,..\,k\Delta T]\) за вполне обозримое время.

    Высоту экспоненты в Ур. 6.1 задаёт \(h(t)\), в классической метадинамике её принимают постоянной и равной \(h_{0}\). В большом временном пределе \(F(\mathbf{s})+V(\mathbf{s},t)\) обращается в константу, поэтому оценка свободной энергии \[F(\mathbf{s})=\const-\lim_{t\to\infty}V(\mathbf{s},t), \tag{6.2}\] т.е. зная, как смещающий потенциал \(V(\mathbf{S},t)\) меняется во времени, можно реконструировать вид поверхности потенциальной энергии [2,3].

    Well-tempered метадинамика

    Для лучшей сходимости метадинамики, высота \(h(t)\) на больших временных масштабах должна уменьшаться, например, по закону: \[ \begin{aligned} h(t) & = & h_{0}\exp\left\{ -\dfrac{V(\mathbf{s}(t),t)}{k\Delta T}\right\} , \end{aligned} \] эту модификацию называют well-tempered метадинамикой, высота гауссианы определяется привнесённым смещением \(V(\mathbf{s}(t),t)\) и фиктивной температурой \(\Delta T\). Если система перешла в новую область ФП, где ещё не был наложен смещающий потенциал, высота добавляемых гауссиан вновь вырастет до значения \(h_{0}\) и будет уменьшаться с ростом \(V(\mathbf{s}(t),t)\) в этой области. Аналогично Ур. 6.2 можно записать оценку \[ F(\mathbf{s})=\const-\left(1+\dfrac{T}{\Delta T}\right)\lim_{t\to\infty}V(\mathbf{s},t). \]

    На практике далеко не всегда удаётся достичь выхода \(V(\mathbf{s},t)\) на постоянное значение — глубина исследования ФП определяется доступным машинным временем, однако, стоит упомянуть, что в момент перехода системы в свободное плавание (Рис 6.2 в) она начнёт быстро дрейфовать по поверхности свободной энергии и может даже совершить прыжок в область ФП вне интересующих нас пределов, об этом важно помнить, чтобы остановить моделирование в подходящий момент.

    Резюмируем. Протокол метадинамики включает несколько шагов: 1. конструируются коллективные переменные \(\mathbf{S}(\mathbf{q})\) — функции координат атомов, цель которых — ёмкое и исчерпывающее описание эволюции системы в процессе моделирования с позиции наблюдения интересующих исследователя событий, иными словами, изменение \(\mathbf{S}(\mathbf{q})\) должно отражать протекание конкретного процесса, поскольку сэмплирование ФП происходит согласованно с пространством КП; 2. выбираются период наложения \(\tau\), начальная высота \(h_{0}\) и ширины \(\sigma_{i}\) гауссиан; 3. проводится компьютерное моделирование со смещающим потенциалом \(V(\mathbf{s},t)\); 4. восстанавливается вид поверхности свободной энергии по изменению \(V(\mathbf{S},t)\) во времени.

    Источники

    1.
    Glowacki D.R., Paci E., Shalashilin D.V. Boxed molecular dynamics: A simple and general technique for accelerating rare event kinetics and mapping free energy in large molecular systems // Journal of Physical Chemistry B. ACS Publications, 2009. Т. 113, № 52. С. 16603–16611.
    2.
    Barducci A., Bussi G., Parrinello M. Well-tempered metadynamics: A smoothly converging and tunable free-energy method // Physical Review Letters. 2008. Т. 100, № 2.
    3.
    Barducci A., Bonomi M., Parrinello M. Metadynamics // Wiley Interdisciplinary Reviews: Computational Molecular Science. Wiley Online Library, 2011. Т. 1, № 5. С. 826–843.